Teoria dell'informazione
Modello di un sistema di trasmissione
Nella trasmissione di informazione da un punto ad un altro dello spazio si può individuare il seguente schema logico.
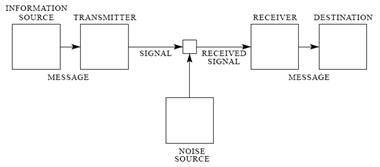
Per spiegare il significato di questi blocchi, si pensi al caso della comunicazione tra una persona che parla e una che ascolta. La persona che sta parlando si può modellizzare come la sorgente di informazione è, le idee che vuole trasferire sono il messaggio, l’apparato vocale è il trasmettitore è cioè quel sistema che trasduce il messaggio e trasmette un segnale. Generalmente il segnale e il messaggio hanno grandezze fisiche diverse. In questo caso il messaggio esiste sotto forma di impulsi elettrici ed è la rappresentazione che si ha di una realtà, ma in questa forma fisica esso non può essere trasferito quindi c’è bisogno di trasformarlo in onde acustiche nel caso di trasmissioni a brevi distanze, o in onde elettromagnetiche se si vogliono raggiungere distanze maggiori o in segni se si vuole memorizzarlo anziché trasmetterlo. Nel caso biologico si può pensare che i geni di un cromosoma affidino il proprio messaggio all’mRNA il quale costituisce il segnale che viaggia dal nucleo verso il citoplasma, dove il segnale è trasdotto nuovamente e interpretato ad opera del ribosoma e dei tRNA. Il canale è quel mezzo in cui si propaga il segnale e può essere l’etere per i suoni o le onde elettromagnetiche, l’ambiente cellulare per un mRNA o il sangue per gli ormoni. Il canale non è di solito, ideale perchè subisce l’influenza del rumore, cioè un evento in grado di degradare il segnale. Nel caso della comunicazione verbale, il rumore può essere dovuto ad altri suoni presenti nell’ambiente che si sovrappongono al segnale e ha l’effetto di rendere difficoltosa o addirittura impossibile la comprensione del messaggio ricevuto. Nella cellula il rumore può essere dovuto alla presenza di enzimi che iniziano a degradare l’mRNA, nel caso di insetti di sesso diverso il vento permette la diffusione del segnale chimico ma se è eccessivo può essere visto come rumore perché a causa dell’eccessiva dispersione rende insufficiente la concentrazione di molecola che giunge all’altro insetto. Anche un inquinante che si diffonde nell’ambiente costituisce del rumore perché viene ricevuto da un organismo e induce delle risposte indesiderate. Il concetto del rumore è applicabile anche alla memorizzazione, si pensi al ritrovamento di un manoscritto la cui decifrabilità dipende dalla conservazione e cioè dalla degradazione subita nel tempo da parte del supporto.
Il ricevitore compie un’operazione opposta a quella del trasmettitore cioè capta il segnale e lo trasduce in messaggio. Nel caso umano è rappresentato dall’apparato uditivo, nel caso biochimico è rappresentato da un recettore. Il destinatario è chi legge e utilizza il messaggio.
La teoria dell’informazione
Lo studio della teoria dell’informazione è stato iniziato da Shannon (1948) il quale ha formalizzato i concetti appena esposti e quelli di comunicazione, quantità di informazione, efficienza e ridondanza che caratterizzano una sorgente che emette un messaggio.
Un messaggio è inteso come una sequenza di eventi o di simboli il cui manifestarsi porta un’informazione. L’informazione è l’interpretazione di un messaggio e quindi quell’evento che elimina l’incertezza in chi lo riceve. Per capire meglio la differenza tra messaggio e informazione, si pensi ad una persona che legge un testo scritto in una lingua che non conosce, questa non ricava dalla lettura alcuna informazione sebbene il testo sia un messaggio scritto in modo corretto. Si nota che il significato ovvero la semantica di un messaggio è relativo a chi lo legge quindi l’informazione non è univoca nei confronti di diversi destinatari. Per assicurare la corrispondenza univoca tra il significato e il messaggio, la sorgente e il destinatario devono essersi accordati preventivamente sulle regole da utilizzare nella trasmissione. A questo scopo servono le regole grammaticali e sintattiche che ci vengono insegnate durante i primi anni di scuola. Per fare un parallelo con ciò che avviene nella cellula possiamo dire che il messaggio contenuto in un gene non è univoco per tutte le specie perché dipende da come i tRNA lo interpretano. Nonostante le regole, nel messaggio umano (scritto, parlato, gesticolato) ci sono ulteriori gradi di libertà che non sono definiti da regole precise e la cui interpretazione dipende in parte dall’esperienza di ciascuno di noi, si pensi al diverso uso del tono della voce o del volume, i quali a parità di parole attribuiscono al messaggio sfumature diverse. La stessa direttiva pronunciata in modi diversi, può apparire come un ordine, un consiglio, un dovere o può rendere l’idea del tempo entro il quale andrebbe eseguita...
L’uso del dialetto all’interno di una lingua, comporta la sostituzione di un certo numero di regole rispetto a quelle più generali della lingua ufficiale, questo ha l’effetto di rendere difficoltosa la comprensione del messaggio da parte di ascoltatori che non ne conoscono quelle regole di interpretazione quindi si può pensare all’uso del dialetto come ad una sorta di criptaggio del messaggio. Quando il dialetto sostituisce tutte le regole del linguaggio ufficiale allora si può parlare a tutti gli effetti di un nuovo linguaggio. I termini e le abbreviazioni usate in certe discipline quali l’elettronica, la chimica ecc… dal punto di vista linguistico possono essere ricondotti ai dialetti. Volendo produrre una rappresentazione grafica di questi concetti possiamo utilizzare la teoria degli insiemi e rappresentare un linguaggio come un insieme di regole.

Un dialetto parlato nei territori interni di una nazione è un insieme costituito da alcune regole del linguaggio ufficiale e altre regole diverse, un dialetto usato nelle zone di frontiera tra due nazioni avrà un numero di regole derivate da entrambe le lingue e altre regole proprie. Il destinatario può conoscere un solo insieme di regole o più, in quest’ultimo caso rientra il bilinguismo. Anche le contaminazioni intese come l’utilizzo di parole estranee alla lingua ufficiale, sono simili ad un dialetto ma a differenza di questo, aggiungono delle nuove regole e non le sostituiscono.
Il concetto di codifica richiama quello della traduzione e indica l’operazione con cui si può passare in modo univoco da un linguaggio ad un altro. Questa corrispondenza può essere eseguita in vari modi e portare nello stesso tempo a vantaggi e svantaggi a seconda di come viene eseguita. Lo studio delle codifiche mira a trovare una relazione tra il tipo di codifica e l’effetto sul segnale emesso. Per fare un esempio di codifica si pensi alla seguente situazione: è notte e dobbiamo trasmettere una risposta del tipo si o no ad un nostro collega che si trova sulla sommità di una collina ad 1Km di distanza da noi. Supponiamo di avere a disposizione due lampade, una verde e una rossa da poter accendere come vogliamo per far capire all’altro la nostra risposta. La codifica consiste nell’essersi preventivamente accordati sulla sequenza del segnale luminoso da produrre per trasmettere uno dei due stati. Il fatto di avere scelto dei segnali luminosi consiste nell’avere fatto una trasduzione del messaggio. Si potrebbe fare una codifica che associa alla risposta ‘si’ una luce verde accesa per 1 secondo, oppure la stessa luce per 30 secondi oppure una certa combinazione di luce verde e rossa tale da creare una sequenza di colori. Per il momento pensiamo che la luce accesa per un secondo ha il vantaggio di rispondere in modo molto veloce ma se in quel momento il nostro collega non stava guardando nella nostra direzione, la comunicazione non sarà andata a buon fine e il malcapitato rimarrà l’intera notte ad aspettare il nostro segnale.
Per definire la quantità di informazione portata da un evento si parte dal caso più semplice e cioè quello di un evento che può assumere solo due stati equiprobabili ovvero di una sorgente che può emettere solo due simboli, ad esempio 0 o 1. In questo caso, l’accadere dell’evento risolve una situazione di incertezza che si aveva rispetto a due situazioni possibili. Un evento di questo tipo si dice che porta una quantità di informazione pari a un bit. Formalizzando la quantità di informazione portata da un evento che può assumere N stati equiprobabili o da una sorgente che può produrre N parole equiprobabili è pari a
i=log2N
Nel caso delle basi del DNA si ha N=4 poiché 4 sono le basi possibili e ogni singola base porta una quantità di informazione pari a 2 bit. Gli amminoacidi sono 20 quindi ogni amminoacido mi permette di distinguere tra 20 stati diversi. Ogni amminoacido porta una quantità di informazione pari a
i=log220=4,32 bit.
Naturalmente se si osserva una sequenza di M eventi ciascuno dei quali può assumere N stati equiprobabili, si osserverà una quantità di informazione maggiore ed esattamente pari a i=log2(NM)
Maggiori sono N e M maggiore è la quantità di informazione portata da una sequenza di eventi.
Ora si pensi al gene che negli eucarioti è organizzato in esoni e in introni. Comunemente si dice che gli esoni portano molta informazione perché codificano e presentano motivi enhancer e silencer per lo splicing mentre e gli introni ne portano molto poca perchè non codificano. In realtà si dovrebbe dire che questi due tipi di sequenze hanno un significato diverso, nel senso che l’evoluzione ha formato un sistema di lettura del pre-mRNA che attribuisce un maggiore significato agli esoni. Si consideri anche che oggi non si conosce pienamente la funzione degli introni e dire che questi hanno scarso significato è rischioso.
Discorso analogo viene fatto quando si legge una sequenza di ammonoacidi compongono un peptide nel senso che non si attribuisce a ciascuno di essi la stessa quantità di informazione. Pensando alla corrispondenza tra la sequenza e la struttura tridimensionale si dice che alcuni amminoacidi sono molto importanti perché formano il sito attivo e tra essi alcuni sono più importanti di altri, cioè portano più informazione, perché una qualsiasi sostituzione si traduce in una modifica notevole della forma del sito attivo. Altri amminoacidi contengono minore informazione perché contribuiscono a formare la struttura generale della proteina, ancora una volta tra questi, alcuni sono più sostituibili di altri nel senso che non modificando la struttura tridimensionale. In questo caso non è corretto dire che alcuni amminoacidi portano più informazione di altri, ma è invece corretto dire che l’insieme di leggi fisiche che costruisce la struttura tridimensionale di una proteina, attribuisce ruoli diversi agli amminoacidi a seconda del tipo e della posizione lungo la sequenza. Questa corrispondenza con le sue regole costituisce un linguaggio; altro linguaggio è quello che fa corrispondere la struttura tridimensionale alla funzione biochimica.

Le regole di questi linguaggi non sono ancora state ben comprese e questo rappresenta uno fra gli obiettivi centrali della proteomica. Un problema ancora più complesso è quello inverso, cioè passare da una desiderata funzione biochimica alla sequenza peptidica che può realizzarla. La difficoltà consiste nel fatto che una sequenza peptidica è come una parola emessa da una sorgente ma le parole possibili sono in numero così elevato che non si riesce a determinarne il significato di tutte ovvero tutte le possibili strutture. Per avere un’idea del numero di parole prodotte da una tale sorgente si pensi che il numero di peptidi diversi costituiti da 10 amminoacidi sono 205 = 3.200.000 e tutti quelli di lunghezza compresa tra 1 e 5 sono 3.368.420.
Per determinare la corrispondenza tra le parole di un linguaggio e il loro significato ci sono in generale due possibilità, la prima è quella detta esaustiva che determina tutte le possibili corrispondenze, la seconda è quella detta deduttiva che si basa sull’estrapolazione di regole generali a partire dalla conoscenza di un numero ridotto di corrispondenze tra parole e significato. Naturalmente la via esaustiva è quella deterministica ma non sempre è possibile seguirla perché a volte non si hanno a disposizione tutti i dati. La via deduttiva mira a trovare un insieme di parole sinonime in modo da poter estrapolare una corrispondenza più ampia, governata da un numero non troppo elevato di regole. Per non troppo elevato si intende minore rispetto a tutte le possibili corrispondenze. Va detto che quanto più il comportamento da modellizzare è fortemente non lineare, tanto meno esistono parole sinonime e tanto meno è adatto il metodo di studio deduttivo.
Dall’osservazione dei linguaggi naturali si nota che i simboli sono organizzati a formare le parole e le parole le frasi. Questa struttura granulare, all’interno di una sequenza sconosciuta, è generalmente evidenziata dalla presenza di due caratteristiche, una è la diversa frequenza associata alla comparsa di simboli o successioni di simboli, l’altra è la correlazione. Ci si può accorgere ad esempio che certe parole compaiono più o meno raramente di altre e altre ancora non compaiono mai, inoltre alcune parole potrebbero comparire o no in funzione di altre parole presenti nella sequenza. La non equiprobabilità e la correlazione definiscono la ridondanza di un linguaggio. Per fare un esempio di ridondanza nella lingua italiana si guardi il grafico seguente.
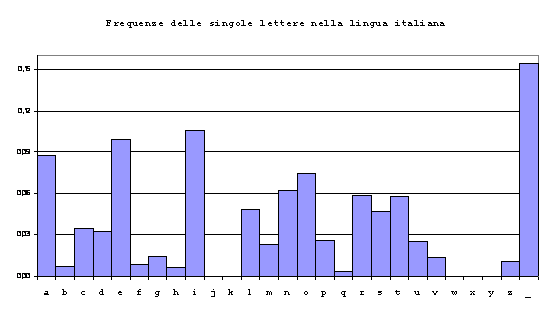
Sono riportate le diverse frequenze associate a ciascun carattere ricavate da un testo sufficientemente lungo. La barra indicata dal trattino indica lo spazio tre le parole. Si nota che i caratteri sono utilizzati in modo diverso, ad esempio le vocali sono in generale più utilizzate delle consonanti. Questo fenomeno costituisce un’evidenza di ridondanza.
Ora si pensi che i caratteri all’interno di una parola non sono disposti in modo casuale, ad esempio se una parola inizia con i caratteri ALB allora in quarta posizione non si troverà un qualsiasi carattere: non potranno seguire C, D, F, G, H, L… perché ALBC non è una sequenza permessa. Allo stesso modo le parole in una frase si troveranno sempre in certi modi e non in altri: non si troverà mai LI CASA o LO CASA. Questi legami tra i caratteri sono l’altro modo del manifestarsi della ridondanza.
Nel caso dei linguaggi naturali, l’individuazione delle parole è resa possibile dagli spazi, ma volendo studiare una sequenza i cui caratteri non sono interrotti, la prima ipotesi da verificare è se essa sia organizzata in parole. Si immagini di essere degli esperti di teoria dell’informazione e di essere alle prese con sequenze di mRNA non conoscendo che esse sono organizzate in codoni. Si comincerebbe con l’ipotizzare che il messaggio contenga parole e si inizierebbe a ricavare la frequenza di tutte le basi per poi passare alle coppie, alle terne e così via, ma non sapendo se esse sono tutte di identica lunghezza si dovrebbero poi provare tutte le combinazioni di parole di varie lunghezze. In questo caso non troveremmo parole proibite almento per lunghezze fino a 10 o 15 basi ma troveremmo delle forti periodicità di frequenze per parole lunghe multipli di tre e si potrebbe ipotizzare che il blocco più piccolo che conserva ancora un significato sia lungo tre nucleotidi. Se avessimo a disposizione tutti i possibili messaggi che la sorgente può produrre, ovvero tutte le possibili sequenze di mRNA che possono esistere in una specie, verosimilmente potremmo ricavare le regole del linguaggio con cui sono formati i messaggi ma nulla potremmo dire sul significato dei messaggi anche perché questa operazione non è univoca.
Poiché solitamente una sorgente di informazione non emette simboli in modo equiprobabile, cerchiamo di modellizzare questo caso più generale al fine di avere una corretta misura della quantità di informazione emessa. Per prima cosa si assume che la sorgente sia un processo stocastico e come tale, descrivibile da un insieme di regole statistiche. Queste vengono ricavate osservando il maggior numero possibile di simboli emessi e ricavando delle frequenze di comparsa per ciscun simbolo e se possibile per ogni parola. Si immagini di aver osservato un messaggio binario e di aver determinato che il simbolo 0 ha una frequenza di comparsa pari a 1/N0 mentre il simbolo 1 compare con una frequenza di 1/N1 dove N=N0+N1 corrisponde al numero totale dei simboli osservati. Da queste frequenze si possono ricavarne delle semplici regole probabilistiche e affermare che la sorgente in esame ha una probabilità P0=1/N0 di emettere 0 e P1=1/N1 di emettere 1.
Se nella formula i=log2N andiamo a sostituire N, si ricava
i0 = log2(1/P0) = - log2(P0) e
i1 = log2(1/P1) = - log2(P1)
che sono rispettivamente la quantità di informazione portata dal simbolo 0 e dal simbolo 1 nel messaggio. Si nota che minore è la probabilità di comparsa di un simbolo, maggiore è l’informazione ad esso associata. Questo è facilmente intuibile perché se si è determinato che statisticamente un simbolo compare molto spesso allora la comparsa del simbolo ad un certo istante è prevedibile, e l’evento ha portato poca informazione perché ha dovuto eliminato la già poca incertezza che avevamo a priori. Al limite l’osservazione che in una sequenza compaia sempre lo stesso evento, fornisce la certezza della comparsa e non lascia nell’osservatore alcuna incertezza. Il fatto di osservare a posteriori proprio quel simbolo, non fornisce alcuna informazione perché avendo già la certezza della sua comparsa, la verifica della comparsa non elimina alcuna incertezza.
Se P0 = 0.1 e P1 = 0.9
i0 = - log2(0.1) = 3.3 bit
i1 = - log2(0.9) = 0.15 bit
Calcoliamo ora la quantità di informazione media per simbolo utilizzando la formula
imedio = P0 * i0 + P1 * i1 [bit per simbolo]
otteniamo
imedio = 0.1 * 3.3 + 0.9 * 0.15 = 0.46 bit
nel caso di simboli equiprobabili otteniamo
imedio = 0.5 * 1 + 0.5 * 1 = 1 bit
Continua... Pagina in costruzione
Bibliografia
1) A Mathematical Theory of Communication, C. E. SHANNON
The Bell System Technical Journal, Vol. 27, pp. 379–423, 623–656, July, October, 1948.
Scarica la presentazione della teoria dell'informazione


