Scitale (www.hranajanto.com)
La crittografia ha l'obiettivo di alterare un messagio in modo concordato tra mittente e destinatario in modo da renderne incomprensibile il significato ai non autorizzati. Esistono due tipi di crittografia, la trasposizione e la sostituzione.
Scitale
(www.hranajanto.com)
La trasposizione consiste nel cambiare posto alle lettere di una frase per cui il destinatario deve risalire alla frase originaria esplorando tutte le trasposizioni procedendo per prove ed errori. Al crescere della lunghezza della frase, il destinatario deve esplorare un numero di anagrammi talmente alto da rendere impossibile risalire alla frase originaria in tempi ragionevoli. Quindi il metodo di trasposizione da un lato garantisce la massima inviolabilità ma dall'altro rende inutilizzabile il messaggio anche da parte del destinatario.
Un semplice meccanismo di criptaggio con una regola ben definita è quello di scrivere alternativamente i caratteri di una frase in due righe e poi unire le righe una dietro l'altra (trasposizione a inferriata).
Es:
volendo criptare la parola
12345678
si scrive ciascun carattere in due righe alternativamente
1357
2468
poi su uniscono le righe ottenendo la parola criptata
13572468
Naturalmente si può pensare a tutte le possibili varianti di questo metodo, come la scrittura su un numero di righe maggiore di due.
meet me near the clock tower at twelve midnight tonite
m e e t m
e n e a r
t h e c l
o c k t o
w e r a t
t w e l v
e m i d n
i g h t t
o n i t e
METOWTEIOENHCEWMGNEEEKREIHITACTALDTTMRLOTVNTE
Scitale
(http://utenti.lycos.it/luposabatini)
La tecnica della sostituzione consiste nel sostituire le lettere dell'alfabeto con lettere diverse dello stesso alfabeto.
Es:
a --> h
b --> m
c --> a
d --> g
e --> r
f --> o
o meglio
plaintext alphabet : abcdefghijklmnopqrstuvwxyz
ciphertext alphabet: TDNUCBZROHLGYVFPWIXSEKAMQJ
In generale in un processo di crittografia si distinguono il metodo di crittografia o algoritmo e la chiave. La chiave definisce i particolari del metodo di crittografia. Un non autorizzato che provasse a decriptare un messaggio può intuire che tipo di algoritmo abbia prodotto la criptazione ma poi si troverebe di fronte a un numero elevatissimo di chiavi per provare a decriptarlo. Un algoritmo che prevede un numero elevatissimo di chiavi affrire maggiori garanzie di sicurezza. Se criptassimo con il metodo della sostituzione avremmo a disposizione miliardi di miliardi di chiavi ovvero di modi diversi per ordinare le lettere dell'alfabeto. Questo garantirebbe la sicurezza perchè pur utilizzando una decriptazione a forza bruta, ovvero provando in modo esaustivo tutte le chiavi, si impiegherebbero tempi lunghissimi per raggiungere l'obiettivo.
C'è però un modo più furbo di decriptare un testo criptato con il metodo della sostituzione. Questo metodo si basa sulla determinazione della frequenza di comparsa dei caratteri dell'alfabeto di una lingua. Immaginiamo di analizzare un lungo testo scritto in lingua italiana e determinare le frequenze di ciascun carattere. Potremmo scoprire che il carattere 'e' compare con la frequenza massima, seguito dal carattere 'a' poi dalla 'i', dalla 'o' ecc... Ora nel testo criptato si ricavano le frequenze dei caratteri e ordiniamo i caratteri in ordine decrescente di frequenza. A questo punto con buona approssimazione il carattere più frequente della lingua italiana corrisponderà al carattere più frequente trovato nel testo criptato. Procedendo per frequenze decrescenti si riduce il numero di tentativi da eseguire per il decriptaggio. Lo studio delle regolarità di una lingua possono aiutare ulteriormente il decriptaggio. Ad esempio ci sono caratteri che non si trovano mai consecutivamente ('aa', 'ee', 'ii', 'qq'...) o si trovano con frequenza molto alta subito dopo altri (dopo 'bb' segue con alta frequenza una 'r', dopo 'pp' segue solitamente 'l'). Quindi lo studio delle frequenze e delle correlazioni tra i caratteri di una lingua possono aiutare molto l'operazione di decriptaggio.
Per rafforzare la sicurezza della cifratura si aggiunsero all'alfabeto simboli senza significato e questi venivano disseminati casualmente nel testo da criptre. Un ulteriore miglioramento della sicurezza è quello di codificare il messaggio prima della cifratura, in pratica si avevano due livelli di criptazione. La codifica si ottiene prima della cifratura, associando alle parole altre parole. Naturalmente la codifica è un'operazione lunghissima perchè implica di sostituire tutte le parole con altre e quindi si tratterebbe di ricostruire una tabella di corrispondenze equivalente a un nuovo dizionario. Tale tabella di conversione sarebbe voluminosa e perciò difficilmente occultabile, inoltre il suo scambio tra mittente e destinatario esporrebbe a rischi di intercettazione.
Un metodo di criptaggio molto efficace è quello di cambiare l'alfabeto cifrante durante la criptazione.
Supponiamo di cifrare lo stesso alfabeto con due diversi alfabeti cifranti:
ABCDEFGHI
sifheabot
qnafpensr
e passare alternativamente da un alfabeto all'altro man mano che si cifrano i caratteri. In questo modo la A corrisponderebbe a volte a una 's' a volte a una 'q'. Analogamente la 'f' corrisponderebbe a volte a una C a volte a una D. Il tentativo di decriptaggio sarebbe enormemente complicato. Ancor più complicato sarebbe se si usassero molti alfabeti cifranti corrispondenti allo stesso alfabeto piano. Questa crittografia si pensava avere un'ottima resistenza al decriptaggio attuato con il metodo dell'analisi delle frequenze e possiede un enorme numero di chiavi. In realtà se nel messaggio criptato si individuano parole ripetute, dalla loro distanza e con adeguate considerazioni si può risalire alla lunghezza della chiave e quindi al numero di alfabeti cifranti utilizzati nel criptaggio. A questo punto si divide il messaggio criptato nel numero di alfabeti trovati e si studia ciascuna parte del messaggio con le considerazioni sulle frequenze e le correlazioni viste precedentemente.
Il punto debole di questa cifratura è la sua natura ciclica ovvero il numero limitato di alfabeti cifranti. La sicurezza massima si otterrebbe con tanti alfabeti cifranti quanti sono i caratteri del messaggio e usando una chiave non corrispondente a una parola avente significato ovvero è meglio usare una parola priva di struttura.
Per decriptare un messaggio creato con una chiave casuale senza ripetizioni si dovrebbe procedere per prove ed errori provando tutte le possibili chiavi casuali, ma ammesso che sia possibile farlo in tempi ragionevoli, si otterrebbero tutti possibili messaggi sbagliati tra cui anche quello corretto. Questo tipo di sistemi viene anche detto cifratura a blocco monouso (one-time pad cipher).
Questo sistema che è teoricamente perfetto ha però alcuni limiti. Ricordando che mittente e destinatario devono preparare delle chiavi lunghissime e ogni volta va distrutta quella parte utilizzata per decifrare il messaggio, c'è il problema di produrre un numero molto elevato di chiavi casuali. Se mittente e destinatario si scambiano una gran quantità di messaggi, in breve tempo essi potrebbero consumare molte migliaia di lettere delle chiavi casuali. Sorge il problema di produrre chiavi casuali lunghissime. Le chiavi con le migliori strutture casuali sono quelle generate basandosi sui fenomeni naturali quali il decadimento radioattivo. Immaginiamo di avere un elemento radioattivo e contare le particelle emesse. Noteremo che l'intervallo di tempo che intercorre tra due emissioni di particelle è del tutto casuale.
Metodo di Montecarlo per la verifica della reale casualità di una serie di numeri
Il sistema del blocco monouso comporta la difficoltà di distribuire le chiavi tra mittente e destinatari, inoltre tutti i soggetti devono conservare una perfetta sincronia nell'utilizzo della chiave. Infatti se il destinatario non ricevesse un messaggio del mittente, il mittente sarebbe più avanti nell'utilizzo della chiave casuale, i due non sarebbero più sincronizzati nell'utilizzare lo stesso punto della chiave casuale e i messaggi sarebbero incomprensibili. La comunicazione diretta dei presidenti americano e russo è protetta da un sistema di questo tipo. Nel 1918 fu creata una macchina per crittografia detta Enigma, in essa l'alfabeto cifrante cambia dopo la cifratura di ogni lettera quindi si effettua una cifratura polialfabetica.
Enigma
Nell'operazione di cifratura si dovrebbero evitare le ripetizioni perché esse rappresentano una regolarità e possono far intuire la struttura del crittogramma. Essa realizzava un enorme numero di alfabetici ciafranti e un enorme numero di chiavi. Grazie all'acquisto di queste macchine le comunicazioni militari tedesche durante la seconda guerra mondiale avevano un elevatissimo grado di sicurezza. Mensilmente le postazioni militari tedesche si scambiavano le chiavi per comunicare tramite Enigma.
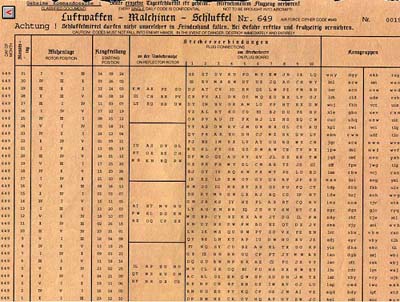Tabella mensile delle chiavi ovvero dell'assetto di Enigma
Alla fine della prima guerra mondiale la Polonia temeva di essere aggredita dai tedeschi e riteneva di vitale importanza comprenderne i messaggi. Grazie ad un traditore tedesco i manuali di enigma furono consegnati ai polacchi. Con i manuali fu possibile ricostruire gli scambiatori di enigma e realizzare repliche di enigma. Un matematico polacco individuò regolarità quali ripetizioni nell'invio delle chiavi giornaliere (i tedeschi commisero l'errore di cifrare la stessa chiave due volte di seguito per assicurare la ridondanza durante la trasmissione) e concatenazioni di lettere, oltre a intuire che gli effetti del pannello e degli scambiatori di enigma possono essere separati. Egli ridusse drasticamente i tempi di identificazione della chiave giornaliera tanto che in circa un'ora era possibile ricostruire la chiave giornaliera scambiata dai tedeschi. Sfortunatamente nel 1938 i tedeschi aumentarono il numero di chiavi di enigma e la decrittazione polacca divenne inefficiente. Per questo motivo i polacchi non riuscirono a venire a conoscenza dell'imminente attacco tedesco. Alcune settimane prima dell'inizio della seconda guerra mondiale, i polacchi in difficoltà per non riuscire a decriptare i messaggi tedeschi, consegnarono le riproduzioni di enigma agli inglesi e ai francesi. Va detto che i polacchi furono i primi ad assumere matematici tra i criptoanalisti dimostrando che essi erano le figurte più adatte alle operazioni di decriptaggio. In Inghilterra, a Bletchley Park, Alan Turing individuò un punto debole non tanto nella crittazione ma negli operatori di enigma.
Bletchley Park
Uno dei punti deboli sono i cilly: chiavi non generate casualmente ma che riproducevano parole banali come ad esempio tre lettere consecutive sulla tastiera, le iniziali della fidanzata dell'operatore, o l'uso ripetuto nella stessa chiave. Inoltre egli sfruttò il cosiddetto crib: un frammento di testo in chiaro che poteva essere interpretato basandosi su un regolarità quali la provenienza del messaggio, l'ora di rasmissione e l'argomento presunto. Era il caso dell'invio dei bollettini meteoroligici che avveniva con regolarità e conteneva parole fisse. Grazie alle comunicazioni stereotipate si riuscivano ad intuire delle parole in chiaro senza necessità di considerazioni crittoanalitiche. Sfruttando queste regolarità Turing ideò un circuito elettrico in grado di ridurre i miliardi di possibili assetti del pannello a prese multiple di enigma. Grazie a Turing una buona parte dei messaggi tedeschi durante la seconda guerra mondiale venne decrittata. Solamente le forze navali tedesche avevano un sistema enigma particolarmente efficiente che sfuggiva al decriptaggio. A causa di questo l'offensiva dei sommergibili U-boot fu particolarmente efficace.
U-boot U995
A questo punto il governo inglese decise di andare in aiuto dei decriptatori inglesi in difficoltà trafugando le chiavi tedesche. Ad esempio Ian Fleming, il creatore di James Bond, progettò un finto ammaraggio di emergenza vicino ad una nave tedesca con un bombardiere tedesco con a bordo militari inglesi travestiti da tedeschi. Quando la nave tedesca fosse andata in soccorso del bombardiere, i militari inglesi si sarebbero potuti impadronire dei cifrari. Grazie al trafugamento di uno di questi cifrari la marina inglese riuscì ad avere la meglio sugli U-boot. Purtroppo Alan Turing non vide riconosciuto il suo merito nell'aver invertito le sorti della guerra perché egli fù perseguitato per la sua omosessualità, tanto che gli fù negato l'accesso a tutte le informazioni riservate e gli fù impedito di fare ricerca nel campo dei calcolatori elettronici. Fu sottoposto a terapia psichiatrica, sviluppò la depressione e a 42 anni si suicidò con il cianuro. In realtà enigma garantiva si un'elevata sicurezza ma non venne usata nel modo migliore poiché le chiavi di messaggio venivano ripetute, c'erano cillies, limitazioni alle configurazione del pannello prese multiple e degli scambiatori, parole fisse nei testi (cribs). In altre parole la sicurezza non poteva essere affidata solamente a congegni sofisticati. La necessità di decriptare le comunicazioni sempre più sicure richiedeva migliori capacità di calcolo le quali non potevano più essere assicurate da sistemi elettromeccanici. La crittoanalisi diede l'impulso alla nascita di computer e il sistema chiamato Colossus fu il primo esempio di elaboratore elettronico. Essoera reimpiegato a Bletchley (UK) e utilizzava 1500 valvole termoioniche, ma sfortunatamente fu distrutto dopo la guerra.
Colossus
(www.picotech.com)
Solo successivamente venne costruito ENIAC che fu il secondo calcolatore elettronico e non il primo come è comunemente accettato.
ENIAC
Dopo la seconda guerra mondiale non solo i militari ma anche ricercatori universitari e appartenenti a ditte private occuparono dello studio della crittografia e del miglioramento della sicurezza anche cercando di superare l'ostacolo della distribuzione delle chiavi. Su due persone dovessero scambiarsi messaggi criptati e si dovrebbero incontrarsi per scambiarsi le chiavi, e se loro messaggi avessero una certa frequenza e si dovrebbero incontrarsi molto spesso per effettuare lo scambio. Il sistema dell'incontro diretto e abbastanza sicuro ma potrebbero esserci dei contrattempi come ad esempio l'impossibilità di uno dei due di essere presente all'appuntamento, per bloccare le comunicazioni. D'altra parte non ci si potrebbe rivolgere ad un corriere per lo scambio, poiché esso non garantirebbe la necessaria sicurezza. Si doveva trovare un sistema per lo scambio delle chiavi estremamente sicuro e che non implicasse l'incontro fisico del mittente e del destinatario. Un abbozzo di soluzione potrebbe essere il seguente: A vuole mandare un messaggio a B, A chiude il messaggio in una scatola con un lucchetto e la manda a B, B riceve la scatola e gli applica un secondo lucchetto poi la rispedisce ad A, A rimuovere il suo lucchetto dalla scatola e la rispedisce a B, ora B è in grado di rimuovere il suo lucchetto e leggere il messaggio. Questo dimostra che è possibile scambiare un messaggio tra un mittente e un destinatario si ognuno lo cripta con la propria chiave. Questo schema a doppia cifratura sembra aver risolto il problema della distribuzione delle chiavi ma in realtà c'è un problema tecnico: l'ordine delle diciture deve rispettare quello delle cifratura quindi A non può rimuovere il suo lucchetto dalla scatola se prima non rimuove quello di B. Allora si cominciarono a studiare le funzioni unidirezionali: un tipo di funzioni per cui se si inseriscono dei valori all'ingresso è molto facile ottenere un valore in uscita ovvero il risultato, ma invertire questo procedimento ovvero risalire ai valori in ingresso dato il valori di uscita è molto difficile. Si dice che una funzione unidirezionale non abbia funzioni diverse. Un esempio di funzione unidirezionale è la funzione in modulo. La funzione (MOD 5) è quella che per valori di ingresso compresi tre zero quattro restituisce l'identico valore in ingresso poi quando l'ingresso aumenta diventando cinque la funzione si riavvolge ricominciando restituire valori da zero in poi. Vediamo alcuni esempi:
0 MOD 5 = 0
1 MOD 5 = 1
2 MOD 5 = 2
3 MOD 5 = 3
4 MOD 5 = 4
5 MOD 5 = 0
6 MOD 5 = 1
7 MOD 5 = 2
8 MOD 5 = 3
9 MOD 5 = 4
10 MOD 5 = 0
11 MOD 5 = 1
12 MOD 5 = 2
Invertire una funzione di questo tipo non risulta immediato e inoltre il risultato dato da un tentativo di inversione sbagliato non dà alcun suggerimento per migliorare il tentativo di inversione successivo. Ora proviamo a immaginare la funzione
453 ^ X MOD 21997
Scegliere un valore di X e calcolare il risultato di questa funzione risulta molto semplice, ma è molto difficile ad esempio determinare il valore di X per il quale la funzione assuma valore 5187. Nel 1976 ci si rese conto che scegliendo una funzione unidirezionale del tipo
Y ^ X MOD P
Con P numero primo e X < P, mittente e destinatario potevano decidere una chiave senza comunicare tra loro. Infatti sufficiente che A e B si scambino i valori di X e P, per stabilire una chiave segreta, non preoccupandosi del fatto che i valori di X e P possono essere stati intercettati. Vediamo un esempio di come mittente e destinatario si possono scambiare le informazioni per generare una chiave comune ma queste informazioni sono insufficienti a una generica spia per risalire alla chiave: A e B concordano una funzione unidirezionale del tipo
7 ^ X MOD 11
e questa informazione può essere intercettata. poi A sceglie un numero segreto, ad esempio X = 3. Lo inserisce nella funzione unidirezionale
7 ^ 3 MOD 11 = 2
e ottiene 2. Anche B sceglie un numero segreto, ad esempio X = 6 e lo inserisce nella funzione unidirezionale.
7 ^ 6 MOD 11 = 4
A dice a B che il suo numero è 2, B dice ad A che il suo numero è 4. Queste informazioni possono essere intercettate. Ora A usa il numero di B nella funzione unidirezionale
4 ^ 3 MOD 11 = 9
e B usa il numero di A nella funzione unidirezionale ottenendo
2 ^ 6 MOD 11 = 9
ed entrambi hanno ottenuto lo stesso numero ovvero la chiave. Ssi era andati oltre il dogma della crittografia dimostrando che mittente e destinatario potevano accordarsi sulla stessa chiave senza scambiarla esplicitamente. L'unico problema pratico di questo metodo è che mittente destinatario devono non qualche modo riuscire a comunicare contemporaneamente perché se il mittente vuole mandare un messaggio al destinatario e se questo è fuori sede, deve aspettare il suo rientro per generare la chiave comune, tritare il messaggio e inviarlo.
L'evoluzione di questo metodo è basato su una chiave detta asimmetrica. Con una chiave simmetrica il processo di cifratura e decifratura è semplicemente uno l'inverso dell'altro, quindi con la stessa chiave si è in grado sia di cifrare che di decifrare il messaggio.
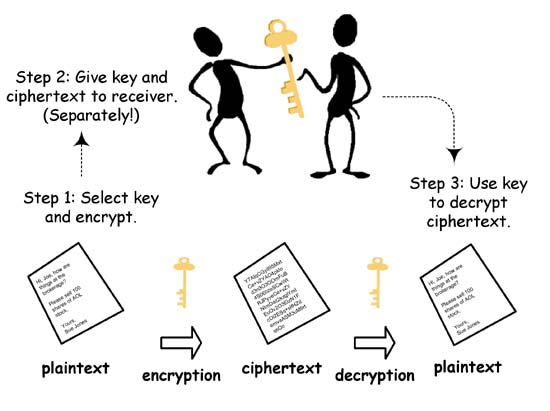Chiave simmetrica
(www.uic.edu)
In un sistema a chiave asimmetrica esistono due chiavi: una per cifrare e l'altra per decifrare. Il mittente che abbia la sola chiave di cifratura, può cifrare il messaggio ma non più decifrarlo. La chiave per cifrare i messaggi è detta chiave pubblica perché essa può essere divulgata in quanto è solo in grado di cifrare. La chiave per decifrare è detta chiave privata ed è quella che va effettivamente tenuta segreta. In questo modo si aggira il problema della necessità della presenza contemporanea di mittente e destinatario per scambiarsi ogni volta la chiave simmetrica.
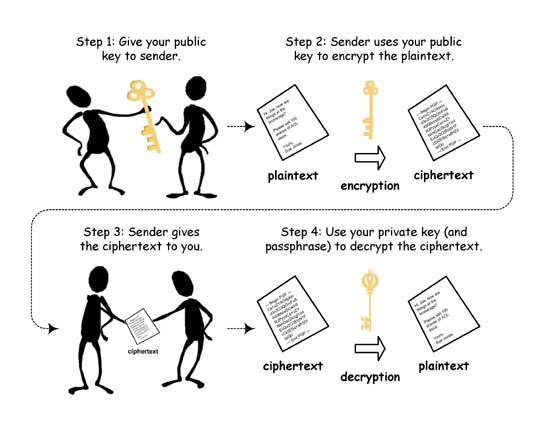Chiave asimmetrica
(www.uic.edu)
A questo punto il problema si riconduceva a trovare una funzione matematica adatta a realizzare una cifratura a chiave asimmetrica. Anche questa volta i numeri primi delle funzioni unidirezionali si rivelarono gli ingredienti giusti. Vediamo brevemente i concetti di questo nuovo sistema: il mittente, A, sceglie due numeri primi X e Y, poi ricava il loro prodotto N.
X * Y = N
N costituisce la chiave crittografica pubblica e può essere diffusa. Se vogliamo scrivere al mittente dobbiamo conoscere la chiave pubblica N e fin qui nessun problema perché N viene resa nota. Il mittente non rende noti i valori X e Y poiché questi costituiscono una chiave privata ovvero sono in grado di invertire la funzione di cifratura. La chiave privata e sicura perché a partire da N è molto difficile ricavare i valori di X e Y in quanto bisogna attuare la scomposizione in fattori primi. Tutto questo viene detto a cifratura a simmetrica RSA dal nome dei suoi inventori (Rivest, Shamir, Adleman). Poiché si scelgono valori di N aventi centinaia di cifre, la scomposizione in fattori primi diventa un'operazione talmente lunga da assicurare un elevato livello di sicurezza alla cifratura, una tale sicurezza che si parla di inviolabilità. Se in futuro si scoprissero metodi molto efficienti per attuare la scomposizione in fattori primi questo renderebbe inutilizzabile l'RSA. Fortunatamente per l'RSA, i matematici cercano questo metodo da un paio di migliaia di anni. Grazie all'RSA il mittente non deve mai comunicare la sua chiave privata e vengono eliminati tutti possibili problemi di intercettazione.
Queste nuove scoperte volevano un'importante problema: la crittografia protegge le comunicazioni dei cittadini onesti ma allo stesso modo può proteggere quelle dei criminali e dei terroristi.
Sebbene questo poteva protegge il diritto individuale alla riservatezza, può rendere i criminali
immuni alle intercettazioni da parte delle forze dell'ordine. È più importante il problema della riservatezza o quello di proteggersi dei criminali ?
Citiamo Zimmermann in quanto creatore del progetto Pretty Good Privacy. Egli voleva risolvere il problema dei tempi non velocissimi richiesti dagli algoritmi RSA, problema che si faceva sentire solo in caso di una fitta comunicazione. Egli usò la codifica a simmetrica RSA e quella simmetrica, la codifica simmetrica e sicura quanto quella asimmetrica ma è molto più veloce anche se è presente il difetto di distribuire le chiavi. Allora si può usare l'RSA per codificare trasmettere soltanto la chiave simmetrica. Mittente e destinatario usano la chiave pubblica RSA per cifrare la chiave simmetrica. Il governo americano, precisamente l'FBI, accusò Zimmermann di essere un trafficante d'armi poiché aveva creato un software crittografico e questo viene definito un'arma da guerra. Fortunatamente il Massachusetts Institute of Technology appoggiò Zimmermann e il procuratore generale rinunciò all'incriminazione. Il software Pretty Good Pcivacy e disponibile all'indirizzo http://www.pgpi.com
Se deciderete di installare questo software assicuratevi che questo tipo di cifratura sia legale nel paese in cui risiede. Se non risiedete negli Stati Uniti assicuratevi di scaricare la versione internazionale del software.
Va detto che la più grande violazione alla privacy individuale è data dal programma Echelon, che intercetta le comunicazioni di ogni cittadino. I programmi di criptazione sono temuti poiché renderebbero inefficace lo spionaggio di Echelon.
Le antenne di Echelon
In questi ultimi anni è emersa la necessità di un'autorità di certificazione. Se A vuole inviare un messaggio a B, deve procurarsi la sua chiave pubblica. Un non autorizzato potrebbe intercettare il messaggio di B diretto ad A e contenente la chiave pubblica, potrebbe modificare il messaggio sostituendo la propria chiave pubblica al posto di quella di B. A ignaro di tutto potrebbe inviare messaggi riservati con la chiave pubblica della spia. È necessario accertarsi di utilizzare proprio la chiave pubblica della persona con cui si vuole comunicare. Le autorità di certificazione si occupano di verificare che una chiave pubblica corrisponda ad una certa persona. Un organismo che si occupa di certificazione ad esempio Verisign, oggi società.
Citiamo una tecnica di crittoanalisi che si chiama tempest attack (approccio tempesta elettromagnetica), esso consiste nel rilevare i segnali elettromagnetici prodotti dalla pressione di ogni tasto della tastiera del computer per poi identificare i tasti che sono stati premuti. Francamente avevo dei dubbi sul fatto che tali debolissimi segnali, per di più immersi nel rumore elettromagnetico, potessero essere captati dai ricevitori installati in un furgone parcheggiato vicino alla nostra abitazione, e conservare ancora un rapporto segnale/rumore sufficientemente buono da poter essere decodificati. Ma sembra che io mi debba ricredere (http://tempestsecurity.blogspot.com/2007_05_01_archive.html).
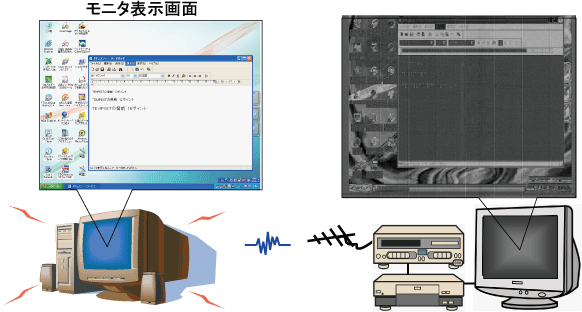Schema di funzionamento di Tempest attack
(http://tempestsecurity.blogspot.com/2007_05_01_archive.html)
Un'altra violazione alla privacy è costituita dalle backdoor inserite dai programmatori nei programmi di criptazione con lo scopo di spiare gli utenti.
Per forzare algoritmi come quello RSA è necessario o migliorare sensibilmente i metodi di scomposizione in fattori primi oppure dotarsi di computer estremamente veloci che eseguono calcoli in poco tempo. Sfortunatamente le attuali prestazioni di computer, e le previsioni dei ritmi di crescita della capacità di calcolo, rendono estremamente sicura la cifratura RSA. Solamente un computer quantistico, ancora irrealizzabile, potrebbe avere la capacità di calcolo sufficiente a risolvere qualsiasi problema in tempi minimi.
Trappola ionica per lo studio di effetti quantistici
http://www.matematiksider.dk/enigma_eng.html
http://plus.maths.org/issue34/features/ellis/